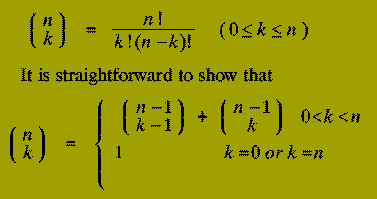
This paradigm is most often applied in the construction of algorithms to solve a certain class of
That is: problems which require the minimisation or maximisation of some measure.
One disadvantage of using Divide-and-Conquer is that the process of recursively solving separate sub-instances can result in the same computations being performed repeatedly since identical sub-instances may arise.
The idea behind dynamic programming is to avoid this pathology by obviating the requirement to calculate the same quantity twice.
The method usually accomplishes this by maintaining a table of sub-instance results.
Dynamic Programming is a
in which the smallest sub-instances are explicitly solved first and the results of these used to construct solutions to progressively larger sub-instances.
In contrast, Divide-and-Conquer is a
which logically progresses from the initial instance down to the smallest sub-instances via intermediate sub-instances. We can illustrate these points by considering the problem of calculating the Binomial Coefficient, "n choose k", i.e.
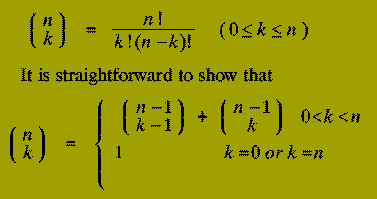
Using this relationship, a rather crude Divide-and-Conquer solution to the problem of calculating the Binomial Coefficient `n choose k' would be:
function bin_coeff (n : integer;
k : integer)
return integer is
begin
if k = 0 or k = n then
return 1;
else
return
bin_coeff(n-1, k-1) + bin_coeff(n-1, k);
end if;
end bin_coeff;
By contrast, the Dynamic Programming approach uses the same relationship but constructs a table of all the (n+1)*(k+1) binomial coefficients `i choose j' for each value of i between 0 and n, each value of j between 0 and k.
These are calculated in a particular order:
(i-1)+(j-1) < (i-1)+j < i+j
The Dynamic Programming method is given by:
function bin_coeff (n : integer; k : integer) return integer is type table is array (0..n, 0..k) of integer; bc : table; i, j, k : integer; sum : integer; begin for i in 0..n loop bc(i,0) := 1; end loop; bc(1,1) := 1; sum := 3; i := 2; j := 1; while sum <= n+k loop bc(i,j) := bc(i-1,j-1)+bc(i-1,j); i := i-1; j := j+1; if i < j or j > k then sum := sum + 1; if sum <= n+1 then i := sum-1; j := 1; else i := n; j := sum-n; end if; end if; end loop; return bc(n,k); end bin_coeff;
The section of the function consisting of the lines:
if i < j or j > k then sum := sum + 1; if sum <= n+1 then i := sum-1; j := 1; else i := n; j := sum-n; end if; end if;
is invoked when all the table entries `i choose j', for which i+j equals the current value of sum, have been found. The if statement increments the value of sum and sets up the new values of i and j.
Now consider the differences between the two methods: The Divide-and-Conquer approach recomputes values, such as "2 choose 1", a very large number of times, particularly if n is large and k depends on n, i.e. k is not a constant.
It can be shown that the running time of this method is
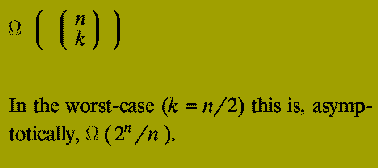
Despite the fact that the algorithm description is quite simple (it is just a direct implementation of the relationship given) it is completely infeasible as a practical algorithm.
The Dynamic Programming method, since it computes each value "i choose j" exactly once is far more efficient. Its running time is O( n*k ), which is O( n^2 ) in the worst-case, (again k = n/2).
It will be noticed that the dynamic programming solution is rather more involved than the recursive Divide-and-Conquer method, nevertheless its running time is practical.
The binomial coefficient example illustrates the key features of dynamic programming algorithms.
Input: A directed graph, G( V, E ), with nodes
V = {1, 2 ,..., n }
and edges E as subset of VxV. Each edge in E has associated with it a non-negative length.
Output: An nXn matrix, D, in which D^(i,j) contains the length of the shortest path from node i to node j in G.
The algorithm, conceptually, constructs a sequence of matrices:
D0, D1 ,..., Dk ,..., Dn
For each k (with 1 < = k < = n), the (i, j) entry of Dk, denoted Dk( i,j ), will contain the Length of the shortest path from node i to node j when only the nodes
can be used as intermediate nodes on the path.
Obviously Dn = D.
The matrix, D0, corresponds to the `smallest sub-instance'. D0 is initiated as:
0 if i=j
D0( i, j ) = infinite if (i,j) not in E
Length(i,j) if (i,j) is in E
Now, suppose we have constructed Dk, for some k < n.
How do we proceed to build D(k+1)?
The shortest path from i to j with only
Either: Does not contain the node k+1.
Or: Does contain the node k+1.
In the former case:
D(k+1)( i, j ) = Dk( i, j )
In the latter case:
D(k+1)( i, j ) = D-k( i, k+1 ) + D-k( k+1, j )
Therefore D(k+1)( i, j ) is given by
Dk(i,j)
minimum
Dk( i, k+1 ) + Dk( k+1, j )
Although these relationships suggest using a recursive algorithm, as with the previous example, such a realisation would be extremely inefficient.
Instead an iterative algorithm is employed.
Only one nXn matrix, D, is needed.
This is because after the matrix D(k+1) has been constructed, the matrix Dk is no longer needed. Therefore D(k+1) can overwrite Dk.
In the implementation below, L denotes the matrix of edge lengths for the set of edges in the graph G( V, E ).
type matrix is array (1..n, 1..n) of integer;
L : matrix
function shortest_path_length (L : matrix;
n : integer)
return matrix is
D : matrix; -- Shortest paths matrix
begin
-- Initial sub-instance
D(1..n,1..n) := L(1..n,1..n);
for k in 1..n loop
for i in 1..n loop
for j in 1..n loop
if D(i,j) > D(i,k) + D(k,j) then
D( i,j ) := D(i,k) + D(k,j);
end if;
end loop;
end loop;
end loop;
return D(1..n,1..n);
end shortest_path_length;
This algorithm, discovered by Floyd, clearly runs in time
Thus O( n ) steps are used to compute each of the n^2 matrix entries.