All Greedy Algorithms have exactly the same general form. A Greedy Algorithm for a particular problem is specified by describing the predicates `solution' and `feasible'; and the selection function `select'.
Consequently, Greedy Algorithms are often very easy to design for optimisation problems.
The General Form of a Greedy Algorithm is
function select (C : candidate_set) return candidate; function solution (S : candidate_set) return boolean; function feasible (S : candidate_set) return boolean; --*************************************************** function greedy (C : candidate_set) return candidate_set is x : candidate; S : candidate_set; begin S := {}; while (not solution(S)) and C /= {} loop x := select( C ); C := C - {x}; if feasible( S union {x} ) then S := S union { x }; end if; end loop; if solution( S ) then return S; else return es; end if; end greedy;
As illustrative examples of the greedy paradigm we shall describe algorithms for the following problems:
The inputs for this problem is an (undirected) graph, G( V, E ) in which each edge, e in E, has an associated positive edge length, denoted Length( e ).
The output is a spanning tree, T( V, F ) of G( V,E ) such that the total edge length, is minimal amongst all the possible spanning trees of G( V,E ).
Note: An n-node tree, T is a connected n-node graph with exactly n-1 edges.
T( V,F ) is a spanning tree of G( V,E ) if and only if T is a tree and the edges in F are a subset of the edges in E.
In terms of general template given previously:
function min_spanning_tree (E : edge_set)
return edge_set is
S : edge_set;
e : edge;
begin
S := (es;
while (H(V,S) not a tree)
and E /= {} loop
e := Shortest edge in E;
E := E - {e};
if H(V, S union {e}) is acyclic then
S := S union {e};
end if;
end loop;
return S;
end min_spanning_tree;
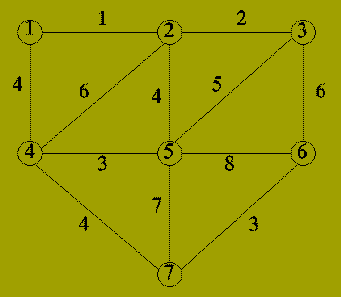
Before proving the correctness of this algorithm, we give an
example of it running.
The algorithm may be viewed as dividing the set of nodes, V, into n parts or components:
{1} ; {2} ; ... ; {n}
An edge is added to the set S if and only if it joins two nodes which belong to different components; if an edge is added to S then the two components containing its endpoints are coalesced into a single component.
In this way, the algorithm stops when there is just a single component
{ 1, 2 ,..., n }
remaining.

| Iteration | Edge | Components |
|---|---|---|
| 0 | - | {1}; {2}; {3}; {4}; {5}; {6}; {7} |
| 1 | {1,2} | {1,2}; {3}; {4}; {5}; {6}; {7} |
| 2 | {2,3} | {1,2,3}; {4}; {5}; {6}; {7} |
| 3 | {4,5} | {1,2,3}; {4,5}; {6}; {7} |
| 4 | {6,7} | {1,2,3}; {4,5}; {6,7} |
| 5 | {1,4} | {1,2,3,4,5}; {6,7} |
| 6 | {2,5} | Not included (adds cycle) |
| 7 | {4,7} | {1,2,3,4,5,6,7} |
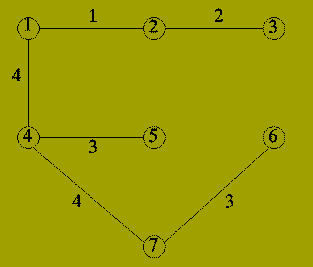
Question: How do we know that the resulting set of edges form a Minimal Spanning Tree?
In order to prove this we need the following result.
For G(V,E) as before, a subset, F, of the edges E is called promising if F is a subset of the edges in a minimal spanning tree of G(V,E).
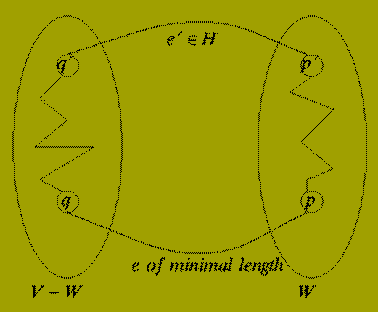
Lemma: Let G(V,E) be as before and W be a subset of V.
Let F, a subset of E be a promising set of edges such that no edges in F has exactly one endpoint in W.
If {p,q} in E-F is a shortest edge having exactly one of p or q in W then: the set of edges F union { {p,q} } is promising.
Proof: Let T(V,H) be a minimal spanning tree of G(V,E) such that F is a subset of H. Note that T exists since F is a promising set of edges.
Consider the edge e = {p,q} of the Lemma statement.
If e is in H then the result follows immediately, so suppose that e is not in H. Assume that p is in W and q is not in W and consider the graph T(V, H union {e}).
Since T is a tree the graph T (which contains one extra edge) must contain a cycle that includes the (new) edge {p,q}.
Now since p is in W and q is not in W there must be some edge, e' = {p',q'} in H which is also part of this cycle and is such that p' is in W and q' is not in W.
Now, by the choice of e, we know that
Length ( e ) < = Length ( e' )
Removing the edge e' from T gives a new spanning tree of G(V,E).
The cost of this tree is exactly
cost( T ) - Length(e') + Length(e)
and this is < = cost(T).
T is a minimal spanning tree so either e and e' have the same length or this case cannot occur. It follows that there is a minimal spanning tree containing F union {e} and hence this set of edges is promising as claimed.
Theorem: Kruskal's algorithm always produces a minimal spanning tree.
Proof: We show by induction on k > = 0 - the number of edges in S at each stage - that the set of edges in S is always promising.
Base (k = 0): S = {} and obviously the empty set of edges is promising.
Step: (< = k-1 implies k): Suppose S contains k-1 edges. Let e = {p,q} be the next edge that would be added to S. Then:
In various forms this is a frequently arising optimisation problem. Input: A set of items U = {u1, u2 ,..., uN}
each item having a given size s( ui ) and value v( ui ).
A capacity K.
Output: A subset B of U such that the sum over u in B of s(u) does not exceed K and the sum over u in B of v(u) is maximised.
No fast algorithm guaranteed to solve this problem has yet been discovered.
It is considered extremely improbable that such an algorithm exists.
Using a greedy approach, however, we can find a solution whose value is at worst 1/2 of the optimal value.
The selection function chooses that item, ui for which
v( ui )
--------
s( ui )
is maximal
These yield the following greedy algorithm which approximately solves the integer knapsack problem.
function knapsack (U : item_set;
K : integer )
return item_set is
C, S : item_set;
x : item;
begin
C := U; S := {};
while C /= {} loop
x := Item u in C such that
v(u)/s(u) is largest;
C := C - {x};
if ( sum over {u in S} s(u) ) + s(x) < = K then
S := S union {x};
end if;
end loop;
return S;
end knapsack;
A very simple example shows that the method can fail to deliver an optimal solution. Let
U = { u1, u2, u3 ,..., u12 }
s(u1) = 101 ; v(u1) = 102
s(ui) = v(ui) = 10 2 < = i < = 12
K = 110
Greedy solution: S = {u1}; Value is 102.
Optimal solution: S = U - {u1}; Value is 110.