In MOTEL we use the
cardinality-based approach proposed by Owsnicki-Klewe
[12] for dealing
with number restrictions. Unfortunately, this approach is incomplete
for languages in which concept disjointness is expressible.
The approach of Baader and Hollunder [1], by
contrast, provides a complete tableau method for 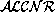 , but has
some disadvantages:
, but has
some disadvantages:
- The approach is not adequate for dealing with large numbers.
Consider the following example: Suppose the universe consists of at
most thirty objects.
If there are at least twenty objects in C and
there are at least twenty objects in D,
then there are at least ten objects in the intersection of C and
D.
The human ability to draw this conclusion is completely independent of
the numbers we are using. Multiplying all numbers occurring in the
example by a factor of 10 wouldn't make it any harder for us come up
with the correct answer. Quite the opposite is true for the tableau method.
- The basic inference mechanism provided by tableau theorem
provers is consistency checking for knowledge bases. This is adequate
for answering queries that can be solved by checking the consistency of
a suitably extended
knowledge base,
for example, for problems like subsumption, instantiation,
and classification.
But the most suggestive class of queries for knowledge bases in
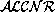 , e.g. the question `How many objects are in C and
D?'
in the example above, cannot even be formulated.
, e.g. the question `How many objects are in C and
D?'
in the example above, cannot even be formulated.
A promising approach to quantitative reasoning with numerical quantifiers
seems to be that of Hustadt, Ohlbach, and Schmidt
[9], who investigate a translation technique
which translates modal logics with graded modalities into a fragment
of many-sorted first-order logic.
For, 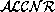 expressions can be associated directly with modal
expressions.
expressions can be associated directly with modal
expressions.


Next: Probabilistic Reasoning
Up: The MOTEL Knowledge Representation System
Previous: Multi-Modalities
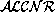 , but has
some disadvantages:
, but has
some disadvantages:
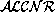 , but has
some disadvantages:
, but has
some disadvantages:
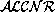 , e.g. the question `How many objects are in C and
D?'
in the example above, cannot even be formulated.
, e.g. the question `How many objects are in C and
D?'
in the example above, cannot even be formulated.
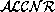 expressions can be associated directly with modal
expressions.
expressions can be associated directly with modal
expressions.