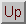.
.
There are at least two reasons why it is interesting to incorporate reason maintenance into a system like the one proposed here. The first is, that it may prove valuable not to dispose of the answers found to queries, but to keep them in order to be able to respond faster if the same queries or instances thereof occur again (similar to the use of lemmata in mathematics). As the knowledge base, however, is of dynamic nature, lemmata are only useful if their origins are remembered. The second reason is that we can't be sure that a knowledge base is globally consistent. So it is worthwile looking for nogoods and reporting them, so that the master component is aware of them, or at least it can be guaranteed that in a single `explanation' (proof) no inconsistent material is used (a kind of paraconsistency).
Fehrer [5] shows how a reason maintenance system
based on an arbitrary basic logic can be described logically.
He also shows there, how an inference system can be
obtained, given a calculus (axioms and set of inference rules)
for the basic logic.
As a special case we can get a system for  .
.
At this stage this result is only of theoretical interest. The main
advantage for using terminological logics, instead of
full first order logics, lies in the fact that they have efficient algorithms
for decidable fragments. The compound
logic resulting from putting the reason maintenance onto 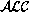 unfortunately cannot always make use of these algorithms
(If we are content with only keeping track of the origins of
lemmata generated so far, there is no problem, for the derived
calculus inherits all the important properties from its ancestor,
so the algorithms can be adapted in a simple manner).
This is
in essence due to the fact that in order to check for nogoods
we have to generate all possible derivations of the falsum.
If, however, we start with a possibly inconsistent knowledge base
some proof strategies do not yield all possible derivations,
for example, strategies incorporating set of support.
But, since decidability as well as completeness is preserved in
the compound system, it should be possible to devise algorithms
with acceptable properties for that task.
unfortunately cannot always make use of these algorithms
(If we are content with only keeping track of the origins of
lemmata generated so far, there is no problem, for the derived
calculus inherits all the important properties from its ancestor,
so the algorithms can be adapted in a simple manner).
This is
in essence due to the fact that in order to check for nogoods
we have to generate all possible derivations of the falsum.
If, however, we start with a possibly inconsistent knowledge base
some proof strategies do not yield all possible derivations,
for example, strategies incorporating set of support.
But, since decidability as well as completeness is preserved in
the compound system, it should be possible to devise algorithms
with acceptable properties for that task.
At the moment, MOTEL allows the removal of terminological and assertional sentences from the knowledge base. For example, if our knowledge base contains the assertional sentence assert_ind(a,and([C,D])), we are able to remove it using the command delete_ind(a,and([C,D])). But it is not possible to remove a part of the assertional sentence using for example delete_ind(a,C). Intuitively, the later command should result in a knowledge base still containing assert_ind(a,D)).